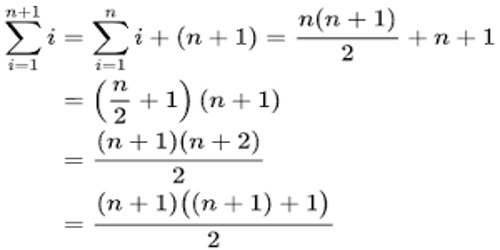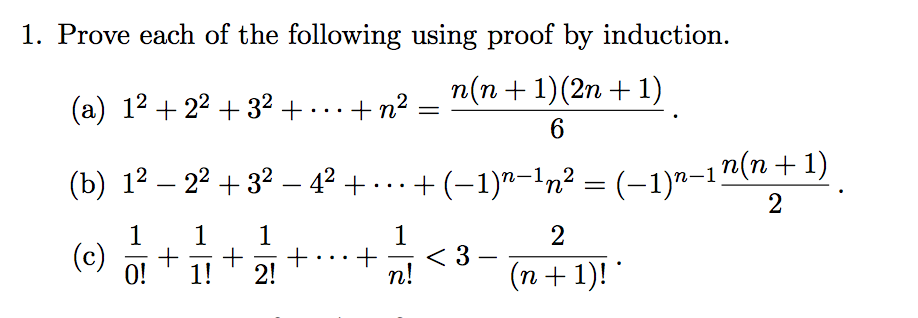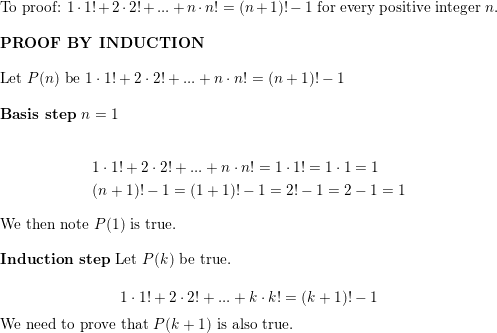Proof By Induction N N 1 2

This one doesn t start at n 1 and involves an inequality instead of an equation.

Proof by induction n n 1 2. Did not show it is true for any values. A proof by induction consists of two cases. There is a pitfall to avoid here. If you graph 4 x and 2 x on the same axes you ll see why we have to start at n 5 instead of the customary n 1.

These two steps establish that the statement holds for every natural number n. The given statement let p n. For n 5 4n 2 n. 2n n n 1 step 1.

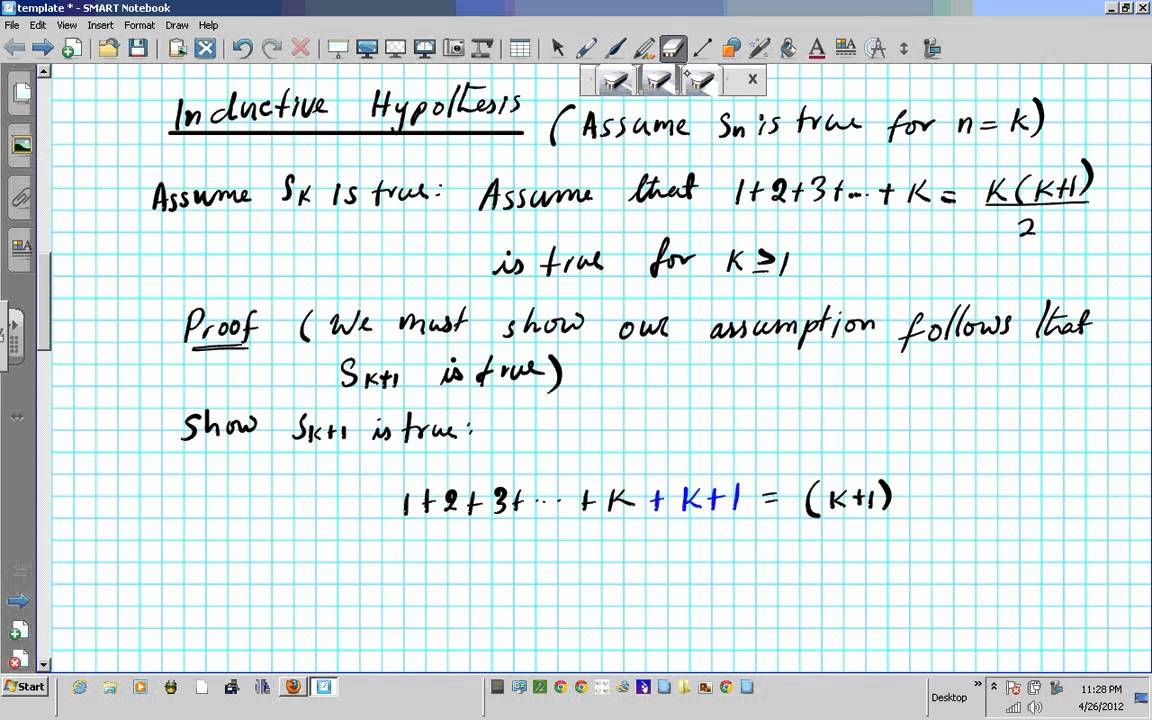
The second case the induction step proves that if the statement holds for any given case n k then it must also hold for the next case n k 1. Epic collection of mathematical induction. N n n 1 2 step. Show the equation is true for n 1 n 2.

N n n 1 2 for n n is a natural number step 1. Is the set of integers for n infinite. An example showing how to do a proof by mathematical induction show that for all n 2 4 6. Here is a more reasonable use of mathematical induction.

N 1 means the first value of the expression on the left side. The first the base case or basis proves the statement for n 0 without assuming any knowledge of other cases. 1 2 3. In this case 2.

Show that given any positive integer n n 3 2 n yields an answer divisible by 3. N 3 2 n is divisible by 3.